728x90
반응형
import numpy as np
import matplotlib.pyplot as plt
# 분산
list1 = [5,8,6,10,1]
target1 = [0,1,2,3,4]
n1 = np.array(list1)
t1 = np.array(target1)
m1 = n1.sum()/5
print(m1)
plt.scatter(t1, n1)
plt.show()
# 9.2 분산
# 3.03 표준편차 = 분산의 제곱근
# 8 (8 - 6 = 2편차) => 오차율 1.03
# 평균 + 표준편차 + 오차율 = 6 + 3.03 + 1.03 -> 9.03 + 1.03 = 10.06
# ( 2.97, 9.03)
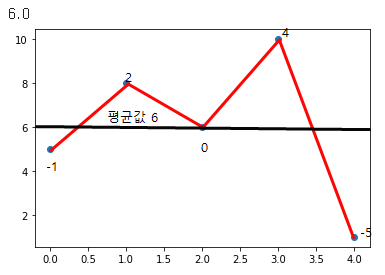
분산 : 1+ 4 + 0 + 16 + 25 (-를 없애기 위해 모두 제곱) = 46 → 46 / 5 = 9.2
표준편차 : 9.2 의 제곱근 = 3.03
- 5번 인덱스에 8이 찍혔을 경우 다음 값 예측하기
8은 평균값 6에서 2만큼 떨어져있다. 평균 값에 대한 편차는 + - 2 이므로 표준 편차의 오차율 1.03
→ 각각의 값은 3.03(표준편차 값) 만큼 떨어져 있어야 하지만 갑자기 8이 들어오게 된다면 8은 '2' 밖에 떨어져 있기 때문에 3.03의 표준편차 값이 바뀌게 된다 따라서 8이 들어갈 경우 2의 편차, 1.03 의 오차율을 그 다음값에 반영 시켜 표준편차 값을 3.03을 만들면 된다.
그 다음값은!! → 평균 + 표준 편차 + 오차율 로 하면 된다.
분산은 표준편차를 찾기위해, 표준 편차는 오차율을 찾기 위해, 오차율은 평균으로 회귀를 시킬 수 있다.
회귀는 이전데이터를 보고 새로운 데이터를 예측할 수 있다. → 그렇기 때문에 우리는 분산과 표준편차를 사용한다.
정규 분포 - 위키백과, 우리 모두의 백과사전
확률론과 통계학에서 정규 분포(正規 分布, 영어: normal distribution) 또는 가우스 분포(Gauß 分布, 영어: Gaussian distribution)는 연속 확률 분포의 하나이다. 정규분포는 수집된 자료의 분포를 근사하는
ko.wikipedia.org

import numpy as np
import matplotlib.pyplot as plt
# 원데이터
# 분산
list1 = [5,8,6,10,1]
target1 = [0,1,2,3,4]
n1 = np.array(list1)
t1 = np.array(target1)
# 1. 평균
m1 = n1.sum()/5 # mean(), sum()
print(m1)
print("="*50)
# 2. 분산 1. (n1 - m1) 2. 거듭 제곱 3. 합치고 4. 전체개수로 나누기
# 1. (n1 - m1) → [5,8,6,10,1] - [6] = [-1,2,0,4,-5]
# 2. [1,4,0,16,25]
# 3. 46
# 4. 9.2
b1 = np.square(n1-m1).mean()
b2 = ((n1-m1)**2).mean()
print(b1)
print("="*50)
print(b2)
print("="*50)
# 3. 표준 편차 1. 분산의 제곱근(루트) → numpy에서는 np.std(원래값) # 정규분포
# 1. 3.03
s1 = np.std(n1)
print(s1)
print("="*50)
s2 = np.sqrt(b1)
print(s2)
print("="*50)
# 표준 점수 mean(), std() → (원점수 - 평균) / 표준편차
# 1. 원점수 - 평균 = [-1,2,0,4,-5] 2. [-1,2,0,4,-5] / 표준 편차 [3.03] → std()
# 1. [5,8,6,10,1] - [6] = [-1,2,0,4,-5]
# 2. [-1,2,0,4,-5] / [3.03] = [-0.330033 0.66006601 0. 1.32013201 -1.65016502]
# 표준점수를 사용하는 이유?
# 변별력을 위해서 점수는 표준화 해야한다.(A 50점, B 90점)
# 표준점수로 변경하면 데이터가 스케일링 된다.
# A C고 - 내신 성적 영어 50점 C고 영어 평균 = 55점 / 표준 편차 = 20
# B D고 - 내신 성적 영어 90점 D고 영어 평균 = 95점 / 표준 편차 = 40
# 서울대학교 (A = 50, B = 90) A (50 - 55) / 20 = -0.25 B (90 - 95) / 40 = -0.125
n1_scaled = (n1 - m1.mean()) / np.std(n1)
print(n1_scaled)
print("="*50)
n2_scaled = (n1 - m1) / s1
print(n2_scaled)
print("="*50)
plt.scatter(t1, n1)
plt.show()
# 9.2 분산
# 3.03 표준편차 = 분산의 제곱근
# 8 (8 - 6 = 2편차) => 오차율 1.03
# 평균 + 표준편차 + 오차율 = 6 + 3.03 + 1.03 -> 9.03 + 1.03 = 10.06
# ( 2.97, 9.03)
728x90
반응형
'Programming > Machine Learning' 카테고리의 다른 글
| Machine Learning 3-2강 - AWS 가입, Docker / 다중 회귀, 특성 공학 (0) | 2021.11.02 |
|---|---|
| Machine Leaning 3 - 1강 - 결정 계수 , 과소 • 과대 적합 , 경사 하강법 (0) | 2021.10.28 |
| Machine Leaning 2-1강 - split , shuffle, index (0) | 2021.10.27 |
| Machine Learning 1강 - 최근접 이웃(KNeighborsClassifier) (0) | 2021.10.27 |