농어의 길이와 무게 데이터
농어의 길이와 무게 데이터. GitHub Gist: instantly share code, notes, and snippets.
gist.github.com
import numpy as np
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
1000.0])
import matplotlib.pyplot as plt
plt.scatter(perch_length, perch_weight)
plt.show()
# 특성 = 길이
# 예측 = 무게
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
perch_length, perch_weight, random_state = 42
)
# 사이킷런으로 훈련할려면 2차원으로 변경해야한다.
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)
print(train_input.shape, test_input.shape)
from sklearn.neighbors import KNeighborsRegressor
# 모델선택
knr = KNeighborsRegressor()
# 훈련 (훈련 데이터)
knr.fit(train_input, train_target)
# 검증 (검증 데이터)
# (훈련) - 과소 적합, 과대 적합
print("훈련세트 결정계수 : ",knr.score(train_input, train_target)) # 결정 계수 R^2 (0~1)
print("테스트세트 결정계수 : ",knr.score(test_input, test_target)) # 결정 계수 R^2 (0~1)
# 설명된 분산 / 전체 분산 (설명된 분산 + 설명할 수 없는 분산) = 결정계수
# 훈련 100, 테스트 50 → 완전 과대 적합
# 훈련 50, 테스트 100 → 과소 적합
# 훈련 95.4, 테스트 95.4 → 우리가 찾아야하는 결정 계수
# 훈련 70.5, 테스트 69.5 → 둘다 과소 적합
과대적합과 과소적합
훈련 세트와 검증 세트는 모델의 과대적합(overfitting), 과소적합(underfitting)이라는 문제와 깊은 연관이 있다. 과대적합과 과소적합이란 과대적합이란 모델이 훈련 세트에서는 좋은 성능을 내지만
ukb1og.tistory.com
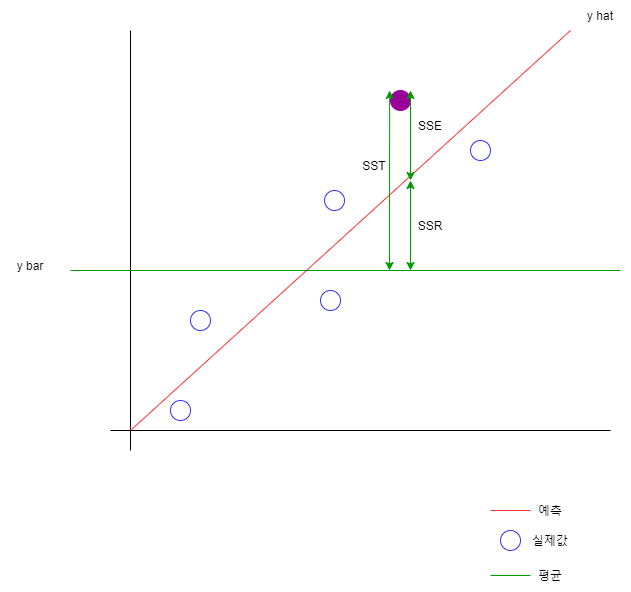
- SSR : Regression sum of squares (설명가능한 분산)
회귀선에 위치한 값과 y 평균을 뺀 값의 제곱의 합
SSR = (y hat - y bar)제곱의 합
- SSE : Error sum of squares (설명 할 수 없는 분산)
회귀선에 위치한 값
실제값과 예측값을 뺀 값의 제곱의 합
SSE = (y - y hat) 제곱의 합
- SST : SSR + SSE (전체 분산)
SST = ( y - y bar ) 제곱의 합
R^2 = 1 - (타깃 - 예측)^2 의합 / (타깃 - 평균)^2 의합
R^2 = 설명된 분산 / 설명된분산 + 설명안된 분산
R^2 = SSR / SSR + SSE
R^2 = 1 - SSE / SST

B4. 다항 회귀분석(Polynomial Regression)
##### 13. 다항 회귀분석(Polynomial Regression) - 다항 회귀분석 : 예측자들이 1차항으로 구성된 것이 아닌, 2차항, 3차항 등으로 ...
wikidocs.net
# 과소 적합과 과대 적합이 무엇인지를 설명해주려고 아래 예제를 사용했음
# 이렇게 쓰면 안됨
# 1, 2, 3, 4, 5, 6
knr.n_neighbors = 4
knr.fit(train_input, train_target)
print("훈련세트 결정계수 : ",knr.score(train_input, train_target)) # 결정 계수 R^2 (0~1)
print("테스트세트 결정계수 : ",knr.score(test_input, test_target)) # 결정 계수 R^2 (0~1)
print(knr.predict([[100]]))
# P (우연히 일어날 확률 - 상관관계가 없다)
# P = 5% → 유의하다
# 상관관계가 있다 (길이에 따라 무게는)
# 길이 = 특성(feature) = 독립변인(원인)
# 무게 = 종속적인(결과)
distance, indexes = knr.kneighbors([[100]]) # 100이라는 농어의 길이에 근접하는 이웃의 3개를 리턴
print(train_input[indexes])
plt.scatter(train_input, train_target)
plt.scatter(train_input[indexes], train_target[indexes])
plt.scatter(100, 1033)
plt.show()
# CI (Contiueous Integration : 지속적 통합)
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input, train_target) # 2차 방정식을 찾아낸 것 ( 절편 + 기울기 )
print(lr.predict([[100]]))
print(lr.coef_, lr.intercept_)
plt.scatter(train_input, train_target)
# 39.017 * x + -709.018
# lr.coef_ * 0 + lr.intercept_
plt.plot([15,100],[lr.coef_ * 15 + lr.intercept_, lr.coef_ * 100 + lr.intercept_])
plt.scatter(100,3192)
plt.show()
# 엄청난 과대 적합 (모델을 잘못? 데이터 정재?(특성?, 데이터양이 작나?))
print(lr.score(train_input,train_target))
print(lr.score(test_input,test_target))
경사하강법
경사 하강법(Gradient Descent)
경사 하강법(Gradient Descent) 경사 하강법(Gradient Descent)은 머신러닝 및 딥러닝 알고리즘을 학습...
blog.naver.com
# 완전 과대적합되었다. (특성을 어떻게 할수는 없지만 데이터의 양을 늘릴 수 없을까?)
# 차수가 1차일 때는 직선의 기울기가 나온다.
# 차수가 2차이상일 때는 곡선이 나온다. (x값마다 기울기 다르다.)
# y = 2x제곱 + 1
import numpy as np
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
1000.0])
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
perch_length, perch_weight, random_state = 42
)
# 사이킷런으로 훈련하려면 2차원으로 변경해야 한다.
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)# polynomialfeatures (다항식)
train_poly = np.column_stack((train_input**2,train_input))
test_poly = np.column_stack((test_input**2,test_input))
print(train_poly[:5])
# 선형이 아니라 곡선을 표현하는게 유리한 상태
# 다항 (항 = 차수(degree)) => 차수를 올리면 x좌표마다 기울기가 달라진다. (곡선을 표현할 수 있다.)
# 머신러닝 모델 => 데이터가 많을 수록 유리!! => 더미데이터!! x, x제곱, x3제곱 => 과대적합에 문제가 된다.
# 규제를 해줘야 한다. (규제를 얼마나 해야할까?) - 알고리즘 사용!!
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.coef_, lr.intercept_)
print(lr.predict([[3**2, 3]]))
point = np.arange(15,50)
plt.scatter(train_input, train_target)
# ax + 절편
# ax^2 + bx + 절편
plt.plot(point,lr.coef_[0]*point**2 + lr.coef_[1]*point + lr.intercept_)
plt.scatter(3, 60.60)
plt.show()
# 과소적합
print(lr.score(train_poly,train_target))
print(lr.score(test_poly,test_target))
'Programming > Machine Learning' 카테고리의 다른 글
| Machine Learning 3-2강 - AWS 가입, Docker / 다중 회귀, 특성 공학 (0) | 2021.11.02 |
|---|---|
| Machine Leaning 2-2강 - 분산, 표준편차, 오차율, 회귀, 표준점수 (0) | 2021.10.27 |
| Machine Leaning 2-1강 - split , shuffle, index (0) | 2021.10.27 |
| Machine Learning 1강 - 최근접 이웃(KNeighborsClassifier) (0) | 2021.10.27 |